最終更新日:2024年4月5日
P010
基礎心理統計法
心理学における統計学の基礎、記述統計学について学ぶ単位条件
通信 2単位教員
履修条件
なし
到達目標
心理学統計法は、心理学における研究内容の理解、およびデータ分析のために必要不可欠であり、心理学を学ぶ上で、基礎となる科目である。
本科目では記述統計について扱う。具体的な到達目標は、心理統計法における基礎的な用語や考え方を学び、理解すること、またそれによりデー
タの傾向を適切に表し、分析できるようになることである。
学習成果
心理統計法における考え方や知識を身に付ける。記述統計を学ぶことにより、データの傾向を適切に分析できる。
推測統計につながる知識を得ることができる。心理学実験など、他の心理学の科目にも応用できるようになる。
テキスト教材
吉田寿夫『本当にわかりやすいすごく大切なことが書いてあるごく初歩の統計の本』(北大路書房)(ISBN 978-4-7628-2125-7)
参考図書
山田剛史・村井潤一郎『よくわかる心理統計』(ミネルヴァ書房)(ISBN 978-4-623-03999-9)
石井秀宗・滝沢龍『臨床統計学』(医歯薬出版)(ISBN 978-4-263-26635-9)
評価の要点
心理統計に関する基礎知識を得ているか、データに適切な統計的処理を行え、データの分析ができるかが評価の要点となる。
具体的には統計に関する用語の理解と数値からデータの傾向を読み取ることができるかである。
計算式を覚えるよりも、どのようなデータであるか、どのような分析方法を行うべきか、また分析方法の仕組みについて理解する必要がある。
評価方法と採点基準
科目終了試験で評価を行う。
履修上の注意事項や学習上のアドバイス
計算式自体を覚える必要はないが、式の仕組みを理解できることは望ましい。
適切な方法でデータを分析することはもちろんのこと、重要なことは、算出した数値が何を示しているのかを理解することである。また算出し
た数値から素データの傾向がわかることや、素データの傾向から計算をしなくともおおよその数値が推測できることは、今後データを分析する
上で必要な能力である。
レポート解答にあたり、Excelやその他の統計ソフト、計算機を使用して構わない。
手計算で行う必要はないが、解答用紙の裏や別紙にて途中式がある場合は部分点を考慮することがある。
レポート課題
提出数 2第1課題
第1設題
※計算結果(数値)を解答する場合は、小数点第3位を四捨五入し、第2位まで記入すること
1 1.下記の1から8の尺度を答えてください。
①体重 ②電話番号 ③大相撲の番付(横綱、大関、関脇) ④年号(西暦) ⑤時間 ⑥性別 ⑦偏差値 ⑧血液型
2.尺度は一般的には、(1)>(2)>(3)>(4)の順で水準が高いとみなされている。例えば、12人の身長を測定し、それぞれの身長の値をデータとする場合は(5)のデータといえる。背の高い人から4人ずつグループを作り、背が高いグループ、中間グループ、背の低いグループとした場合、このデータは(6)のデータといえる。これらを踏まえると、例えば、間隔尺度でデータを取ると、(7)尺度や(8)尺度の変数としてデータを扱うことも可能であるといえる。
3.下記のデータA、B、C、Dにおける、平均値、中央値、標準偏差、四分位偏差の値を算出してください。それぞれを算出した上で、
素データと数値要約の結果を見比べ、各データの数値要約に適した代表値名と散布度名を解答してください(CのみN=6)。

4.データXは N=8、平均値が8.5、標準偏差が2.2のデータである。1このデータXのすべての値に5を足したときの平均値と標準偏
差について答えてください。2このデータXのすべての値を3倍したときの平均値と標準偏差について答えてください。3すべてのデー
タに5を足した場合(+5)とすべてのデータを3倍した場合(×3)では、どちらの分布の幅が広いと言えるでしょうか。
5.次の1から4のケースについて、知能検査Aの信頼性について高いか、低いかの判断を行ってください。
1、ある人が、知能検査(A)と知能検査(B)により、知能指数を測定したところ、2つの検査の知能指数が大きく異なった。
2、ある人が、知能検査(A)により知能指数を測定し、一定の期間が過ぎてから、もう一度知能検査(A)で測定したところ、知能指数が異 なった。
3、ある人が、知能検査(A)と知能検査(B)により、知能指数を測定したところ、2つの検査の知能指数に大きな違いはなかった。
4、ある人が、知能検査(A)により知能指数を測定し、一定の期間が過ぎてから、もう一度知能検査(A)で測定したところ、知能指数はほぼ同じであった。
6.作図、作表する際の図表のタイトルの位置について答えてください(日本心理学会が発行する「執筆・投稿の手びき(2022年版)」
(URLはhttps://psych.or.jp/manual/)を参照すること)。また作図したデータの横軸が連続量のときに用いるグラフ名について答えてください。
第2課題
第1設題
1 1.下記のデータ①、②、③について、散布図を作成してください。また相関係数を求めてください。
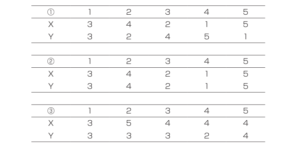
下記のデータX、Yについて、④、⑤の相関係数と回帰直線との一致率について求めてください。

④、⑤のデータをそれぞれ作図した際の回帰直線の一致率について、決定係数という用語を用いて説明してください。また相関係数
をもとにそれぞれの共通点、相違点を比較し、その数値が示す意味について過不足なく説明してください。
2.N=100のデータにおいて、φ係数の値が次の(a)、(b)、(c)となるようにクロス表の( )内に数値を記入してください。また(d)
のφ係数の値を算出してください。
(a)φ=0
(b)φ=0
(c)φ=1
3.下記の文章において、説明があっている場合は「正」を、間違っている場合は「誤」を記入してください。また説明が間違っている
場合は正しい記述に訂正してください。
①相関係数( r )は、0≦ r ≦1の範囲の値を取り、数値が大きくなるとより直線関係が強くなることを示す。
②ピアソンの積率相関係数は計算過程からわかるように、外れ値があっても影響を受けず、算出した値により、2変数間の関係を解
釈することができる。
③AとBの相関関係について、2つの変数(A、B)に第3の変数が影響し、見かけ上の相関関係が想定されることを、分割相関という。
4.あるテストを受けた120人の得点は、平均値が68点で標準偏差が8.0であった。このテストの点数が正規分布していたと仮定し、以下の問に答えなさい。
問1 このテストで68点であった人の標準得点と偏差値を求めてください。
問2 72点以上であった人は何人いるか答えてください。
問3 52点以上であった人は何人いるか答えてください。
問4 このテストで上位20%の境界に該当する人の得点を求めてください。
5.下記のケースA、B、Cにおける対応の有無(①)、独立変数(②)、従属変数(③)、要因数(④)、条件数(⑤)を答えてください。
A.酒の好みについて検討するために、無作為に抽出した30人の成人に、日本酒、ビール、ワインのそれぞれが好きか否かについて
回答を求めた。
B.教授法の効果を検討するために、対象者20人全員に、一斉学習(大集団)、グループ学習(小集団)と個別学習(1対1)で、
それぞれ授業を受けてもらい、学習後のテストの得点を比較した。
C.性格(楽観的か、悲観的か)が依存性の強さ(配点は1から5)に影響するかを調べるために20人を対象としてデータを取り、
それぞれの性格における依存性の強さを比較した。
備考・補足
← 表が横スクロールします →
| 授業回数別教育内容 | 身につく資質・能力 | 学習範囲 (予習・復習を含む) |
|
| 統計について学ぶにあたって | |||
| 妥当性と信頼性 | |||
| 変数とデータ | |||
| 変数の分類 | |||
| 作図、作表 | |||
| 数値要約1(代表値) | |||
| 数値要約2(散布度) | |||
| ピアソンの積率相関係数 | |||
| 相関図の作成 | |||
| クロス表 | |||
| 連関係数 | |||
| 正規分布 | |||
| 線形変換 | |||
| 非線形変換 | |||
| 記述統計と推測統計(適切な検定の選択:テキスト7章) | |||
| 試験 |
